Page 1 sur 2
lois de Neton
Posté : mar. 30 déc. 2014 11:52
par MArie TS
Bonjour j'ai un exercice a faire mais je suis bloquée pouvez vous m'aider svp?
Une bille est immobile par rapport au referentiel terrestre
la bille a une masse m=20g
on considere que g=10N/kg
on negligera la poussée d'Archimede exercée sur la bille;
la bille est suspendue a un pendule et un aimant tire la bille sur le coté
1-faire l'inventaire des forces exterieurs exercées sur la bille
2- determiner la valeur de chaque force lorsque la bille est immobile ...
1-j'ai donc indiqué le systeme et le referentiel et pour le bilan des forces j'ai indiqué :
le poid \(\overrightarrow{P}\)
la tension de la corde \(\overrightarrow{T}\)
l'attraction de l'aimant \(\overrightarrow{A}\)
2- ensuite on a \(\overrightarrow{P}\) =m\(\overrightarrow{g}\) d'ou P=0.2N
d'apres la premiere loi de newton la bille est immobile donc les forces se compensent d'ou somme des forces ext= vecteur nul
mais apres je ne sais pas comment determiner A et T
pouvez vous m'aider s'il vous plait?
Re: lois de Neton
Posté : mar. 30 déc. 2014 12:22
par SoS(38)
Bonjour Marie,
Il faut effectuer un schéma avec les trois vecteurs, schématiser un angle et projeter les vecteurs sur deux axes. Vous aurez alors deux équations littérales.
Re: lois de Neton
Posté : mar. 30 déc. 2014 14:24
par MArie TS
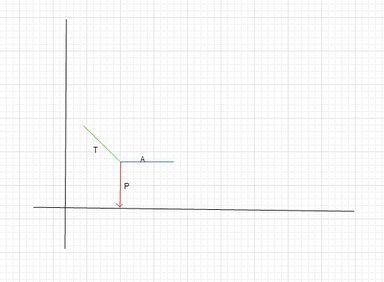
- 00000002.jpg (15.63 Kio) Vu 6492 fois
merci je realise donc ce schémas; j'en deduis que
tan 90°= A/-P
donc que tan 90*-0.2=A
je trouverais donc A=0.399
mais je ne suis pas sure du resultat
Re: lois de Neton
Posté : mer. 31 déc. 2014 00:18
par SoS(38)
Non, il faut reprendre le raisonnement.
L'angle à mettre en jeu est celui entre la tension et la verticale ou entre la tension et l'horizontale.
Il faut ensuite projeter les deux composantes du vecteur tension suivant la verticale et suivant l'horizontale et établir les deux égalités suivant la verticale et l'horizontale.
Re: lois de Neton
Posté : mer. 31 déc. 2014 11:38
par MArie TS
ah merci je ne suis pas sure d'avoir bien compris:
on appele l'angle alpha l'angle entre T et l'horisontale
j'ai aussi:
xA: A
yA: 0
xP: 0
yP: -P
xT: T
yT: -T
apres la je ne suis plus sure: comme les forces se compensent on a:
xA+xT+xP=0
et yA+yT+yP=0
c'est a dire A+T=0 et -P-T=0
donc que T=-P et A=P
mais je pense que c'est faux
Re: lois de Neton
Posté : mer. 31 déc. 2014 14:15
par SoS(38)
je suis d'accord pour les composantes du poids et de l'attraction de l'aimant.
Il y a un problème pour les coordonnées des composantes horizontales et verticales de la tension. Elles dépendent l'une de sin(angle) et l'autre de cos(angle).
Re: lois de Neton
Posté : mer. 31 déc. 2014 15:39
par MArie TS
je comprend ce que vous voulez dire mais je n'arrive pas a l'appliquer:
on cherche x et y de T
avec ce schemas on peut donc dire que tan 90°=yP/xT
c'est tout ce que j'arrive a dire, je ne trouve pas avec quel angle utiliser sin et cos
Re: lois de Neton
Posté : mer. 31 déc. 2014 15:52
par SoS(38)
Pour mieux comprendre, rajoutez l'angle alpha sur le schéma. Vous avez deux segment intéressants intéressants qu'on notera plutot Tx et Ty qui sont tous les deux fonctions de T puis l'un de sin(alpha) et l'autre de cos(alpha)
Re: lois de Neton
Posté : mer. 31 déc. 2014 16:02
par MArie TS
voila mais je ne comprend pas: pour calculer un sinus ou un cosinus il faud connaitre la valeur de l'hypotenuse
ici c'est le vecteur T , on ne le connai pas. voila pourquoi je ne comprend pas ou vous voulez en venir
aidez moi svp
Re: lois de Neton
Posté : mer. 31 déc. 2014 18:06
par SoS(38)
Si, ici, T est la valeur de l'hypoténuse. Vous pouvez alors déduire Tx et Ty dans le triangle rectangle.
Re: lois de Neton
Posté : mer. 31 déc. 2014 18:42
par MArie TS
donc si j'ai bien compris:
Tx: sin Ty/T
Ty:cos Tx/T
je ne pense pas que c'est juste je propose
Tx=Py/tan90
d'ou Ty= cos (Py/tan 90)/T
mais je pense que tout est faux :'(
Re: lois de Neton
Posté : mer. 31 déc. 2014 19:09
par SoS(38)
Revoyez les premières relations, elles ne sont pas homogènes.
cos (alpha) est sans unité donc le rapport de deux valeurs en Newton, idem pour sin(alpha).
Reprenez tout simplement les définitions de base des sin et cos.
Dans ce cas tan(alpha) ne vous sera d'aucun secours car tan(alpha) = Ty/ Tx donc tan(alpha) dépendrait de deux inconnues.
Dans un cas, vous aurez à lier le sin(alpha) et le cos(alpha) aux couples (Tx,T) et (Ty,T).
Re: lois de Neton
Posté : jeu. 1 janv. 2015 17:23
par MArie TS
ok je pense que on obtient:
sin alpha=Ty/T
et cos alpha = Tx/T
si c'est juste pour extraire Tx comment fait on svp?
Re: lois de Neton
Posté : jeu. 1 janv. 2015 18:23
par SoS(38)
Bonsoir et bonne année.
Effectuez simplement des produits en croix.
Re: lois de Neton
Posté : jeu. 1 janv. 2015 18:53
par MArie TS
merci bonne année a tout SOS-physique!
merci beaucoup je trouve au final A=-0.2tan alpha
et T=0.2/sin alpha
est-ce juste?
la dernier question de mon exercice me demande a t=0s on retire subitement l'aimant, la bille se met en mouvement. donner les caractéristiques du vecteur accelération a t=0
si on retire l'aimant sa veut donc dire que A s'annule.la bille va faire un mouvement circulaire uniforme. mais je ne vois pas ce que je peut dire du vecteur acceleration...