Page 1 sur 1
Courant dans un solénoïde et champ magnétique ?
Posté : lun. 13 déc. 2010 16:10
par Pierre (TS)
Bonjour,
Voici un exercice que je ne comprends pas. Voici le sujet :
Une petite aiguille aimantée, tournant librement autour d'un axe vertical, est placée au centre
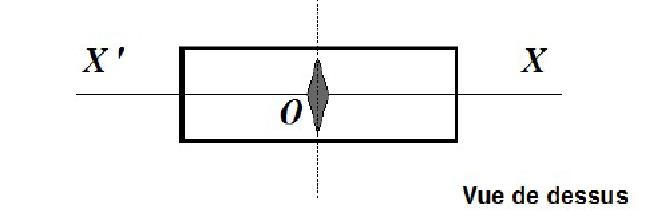
O d'un d'un long solénoïde horizontal, également mobile autour d'un axe vertical passant par
le point O. L'axe X'X du solénoïde est initialement perpendiculaire à l'aiguille aimantée.
Lorsqu'on fait passer un courant d'intensité constante I dans le solénoïde, il faut le faire
tourner d'un angle α pour que l'aiguille soit à nouveau perpendiculaire à l'axe du solénoïde.
On suppose que α0 est l'angle de rotation correspondant à une valeur connue du courant I0.
Quel le est l'expression de l'intensité I du courant ?
Réponse : I=I0.sin(alpha)/sin(alpha0)
Pour moi, la réponse est I = I0.tan(alpha)/tan(alpha0).
Qu'en pensez-vous ?
Merci d'avance pour votre aide.
Re: Courant dans un solénoïde et champ magnétique ?
Posté : lun. 13 déc. 2010 22:10
par SoS(8)
Pierre (TS) a écrit :Bonjour,
Voici un exercice que je ne comprends pas. Voici le sujet :
Une petite aiguille aimantée, tournant librement autour d'un axe vertical, est placée au centre
O d'un d'un long solénoïde horizontal, également mobile autour d'un axe vertical passant par
le point O. L'axe X'X du solénoïde est initialement perpendiculaire à l'aiguille aimantée.
Lorsqu'on fait passer un courant d'intensité constante I dans le solénoïde, il faut le faire
tourner d'un angle α pour que l'aiguille soit à nouveau perpendiculaire à l'axe du solénoïde.
On suppose que α0 est l'angle de rotation correspondant à une valeur connue du courant I0.
Quel le est l'expression de l'intensité I du courant ?
Réponse : I=I0.sin(alpha)/sin(alpha0)
Pour moi, la réponse est I = I0.tan(alpha)/tan(alpha0).
Qu'en pensez-vous ?
Merci d'avance pour votre aide.
Bonsoir Pierre,
Tout à fait d'accord avec vous ! je vous livre mon raisonnement d'après l'énoncé que vous me soumettez :
Re: Courant dans un solénoïde et champ magnétique ?
Posté : mar. 14 déc. 2010 07:49
par Pierre (TS)
Bonjour et merci pour votre réponse.
Pour confirmer tout cela, voici les schémas associés au sujet (je n'avais pas pu les joindre hier).
Confirmez-vous toujours que : I = I0.tan(alpha)/tan(alpha0) ?
Merci d'avance.
SoS(8) a écrit :Pierre (TS) a écrit :Bonjour,
Voici un exercice que je ne comprends pas. Voici le sujet :
Une petite aiguille aimantée, tournant librement autour d'un axe vertical, est placée au centre
O d'un d'un long solénoïde horizontal, également mobile autour d'un axe vertical passant par
le point O. L'axe X'X du solénoïde est initialement perpendiculaire à l'aiguille aimantée.
Lorsqu'on fait passer un courant d'intensité constante I dans le solénoïde, il faut le faire
tourner d'un angle α pour que l'aiguille soit à nouveau perpendiculaire à l'axe du solénoïde.
On suppose que α0 est l'angle de rotation correspondant à une valeur connue du courant I0.
Quel le est l'expression de l'intensité I du courant ?
Réponse : I=I0.sin(alpha)/sin(alpha0)
Pour moi, la réponse est I = I0.tan(alpha)/tan(alpha0).
Qu'en pensez-vous ?
Merci d'avance pour votre aide.
Bonsoir Pierre,
Tout à fait d'accord avec vous ! je vous livre mon raisonnement d'après l'énoncé que vous me soumettez :
- img1.jpg (8.06 Kio) Vu 3174 fois
Re: Courant dans un solénoïde et champ magnétique ?
Posté : mar. 14 déc. 2010 08:08
par SoS(8)
Nous sommes bien d'accord, ce que j'ai noté A représente le champ magnétique terrestre (en fait la composante horizontale donnée par la boussole); B est le champ magnétique créé au centre du solénoïde et BR la résultante de ces deux champs. Nos schémas sont donc parfaitement compatibles et je maintiens ma position, il s'agit bien, en toutes rigueur de tangentes. Maintenant, si l'angle \(\alpha\) est petit, on peut toujours confondre tangente et sinus... mais je ne vois pas l'intérêt...
J'espère vous avoir aidé, n'hésitez pas à revenir en cas de besoin...
Re: Courant dans un solénoïde et champ magnétique ?
Posté : mar. 14 déc. 2010 16:16
par Pierre (TS)
Merci beaucoup !
Bonne semaine !
SoS(8) a écrit :Nous sommes bien d'accord, ce que j'ai noté A représente le champ magnétique terrestre (en fait la composante horizontale donnée par la boussole); B est le champ magnétique créé au centre du solénoïde et BR la résultante de ces deux champs. Nos schémas sont donc parfaitement compatibles et je maintiens ma position, il s'agit bien, en toutes rigueur de tangentes. Maintenant, si l'angle \(\alpha\) est petit, on peut toujours confondre tangente et sinus... mais je ne vois pas l'intérêt...
J'espère vous avoir aidé, n'hésitez pas à revenir en cas de besoin...