Page 1 sur 2
La montgolfière
Posté : dim. 6 avr. 2014 00:57
par Maxime
Bonjour, pourriez-vous m'aider à résoudre cet exercice s'il vous plaît ?
C'est une action répartie agissant sur la montgolfière, modélisée par une force appelée poussée d'Archimède, qui explique son mouvement vertical. La poussée d'Archimède a une direction verticale et est dirigée vers le haut.
1. Construire le diagramme objet-interactions relatif à la montgolfière dans l'air.
Je pense que c'est comme ça.
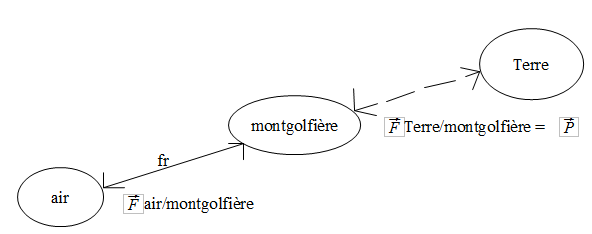
- image.PNG (9 Kio) Vu 14205 fois
2. Modéliser, sur un schéma, sans souci d'échelle, les actions mécaniques par des forces en précisant leurs noms et leurs caractéristiques.
-Dans le cas où la montgolfière a un mouvement vertical ascendant ;
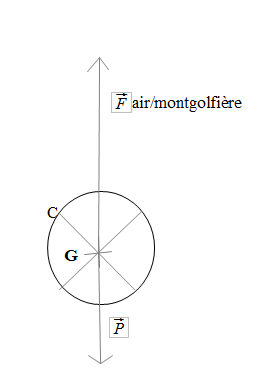
- image.PNG (6.49 Kio) Vu 14205 fois
Poids \(\vec{P}\) de la montgolfière : point d'application : centre de gravité G
direction : verticale
sens : vers le bas
norme : 24 525 N
\(\vec{F}\) air/montgolfière : point d'application : point de contact C entre la montgolfière et l'air
direction : verticale
sens : vers le haut
norme : 24 525 N
Pourriez-vous me dire si mon exercice est juste s'il vous plaît ?
Merci d'avance.
Re: La montgolfière
Posté : dim. 6 avr. 2014 09:28
par SoS(13)
Bonjour Maxime,
Vous êtes dans l'esprit de ce que l'on attend dans cet exercice.
Cependant, concernant la poussée d'Archimède, que l'on vous dit être une force répartie au même titre que le poids, vous ne pouvez lui donner un point d'application C point de contact, mais plutôt un point central (appelé centre de carène) qui correspond plus ou moins au centre de gravité comme vous l'avez représenté sur le schéma.
D'autre part, je ne sais d'où provient la valeur commune que vous attribuée aux normes des forces, d'autant plus que votre schéma représente des forces de normes différentes.
Re: La montgolfière
Posté : dim. 6 avr. 2014 12:10
par Maxime
Merci, donc j'enlève le point de contact C et je remplace le centre de gravité G par le centre de carène. C'est bien ça ?
Mes normes proviennent de la masse moyenne d'une montgolfière (2 500 kg).
P = m \(\times\) G
P = 2 500 \(\times\) 9, 81
P = 24 525 N
Re: La montgolfière
Posté : dim. 6 avr. 2014 12:23
par SoS(13)
Vous ne remplacez pas G par C, mais vous les superposez.
Pour donner la norme de la poussée d'Archimède, il faut la calculer à partir de sa définition, tout comme vous avez fait avec le poids.
Connaissez-vous cette définition ?
Re: La montgolfière
Posté : dim. 6 avr. 2014 13:58
par Maxime
Non, je ne connais pas cette définition.
Re: La montgolfière
Posté : dim. 6 avr. 2014 14:06
par SoS(13)
La poussée d'Archimède a une norme égale au poids de l'air dont la montgolfière occupe la place.
Cela vous permet-il de la calculer ?
Re: La montgolfière
Posté : dim. 6 avr. 2014 14:09
par Maxime
Je ne vois pas comment la calculer.
Re: La montgolfière
Posté : dim. 6 avr. 2014 14:38
par SoS(13)
L'expression est \(\rho\)Vg
Avez-vous le volume occupé par la montgolfière ?
Re: La montgolfière
Posté : dim. 6 avr. 2014 15:00
par Maxime
Non, je n'ai pas le volume occupé par la montgolfière.
Re: La montgolfière
Posté : dim. 6 avr. 2014 15:23
par SoS(13)
Donc vous ne pouvez pas calculer la norme de la poussée d'Archimède !
Re: La montgolfière
Posté : dim. 6 avr. 2014 16:23
par Maxime
Le volume moyen occupé par une montgolfière est 2 200 \(m^{3}\).
Re: La montgolfière
Posté : dim. 6 avr. 2014 16:38
par SoS(13)
Donc vous pouvez réaliser le calcul de la poussée d'Archimède.
La lettre \(\rho\) représente la masse volumique de l'air de valeur 1,3 kg/m\({^3}\)
Re: La montgolfière
Posté : dim. 6 avr. 2014 16:48
par Maxime
Je trouve 2 860 kg.
Re: La montgolfière
Posté : dim. 6 avr. 2014 16:57
par SoS(13)
Je suppose que vous me parlez de la masse de l'air dont la montgolfière occupe la place.
Il vous reste à calculer le poids correspondant et vous aurez ainsi la valeur de la poussée d’Archimède.
Re: La montgolfière
Posté : dim. 6 avr. 2014 17:01
par Maxime
Je parle effectivement de la masse de l'air dont la montgolfière occupe la place.
P (en N) = m (en kg) * G
P = 2 860 * 9, 81
P = 28 056, 6 N